Bu makalede, bir başka klasik FM demodülasyon devresini inceleyeceğiz: Şekil 1’de gösterilen Foster-Seeley ayırıcısı.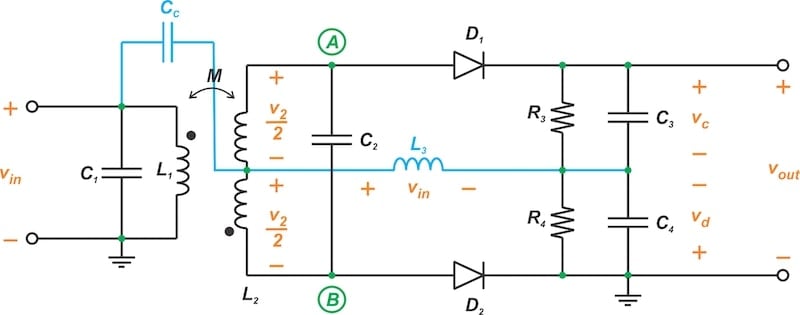
Rezonansın üzerindeki frekanslar için bu devrenin çıkış voltajı pozitiftir. Rezonansın altındaki frekanslar için çıkış voltajı negatiftir. Foster-Seeley ayırıcısının frekans tepkisi Şekil 2’de görülebilir.

Şekil 2. Foster-Seeley ayırıcısının tipik frekans tepkisi.
Foster-Seeley ayırıcısının bu tepkiyi nasıl sağladığı, şemasından ilk bakışta anlaşılamayabilir. Açıklığa kavuşturmak için, devrenin temel bileşenlerinin işleyişini inceleyeceğiz. Ardından, öğrendiklerimizi temel alarak devrenin genel işlevselliğini açıklayacağız.
Öncelikle bir seri RLC devresinin rezonans frekansına yakın davranışını inceleyelim ve özellikle de bu devrenin ortaya çıkardığı faz kaymasına odaklanalım.
Bir RLC Devresinin Faz Kaymasını Anlama
Şekil 3, yukarıdaki şematikteki L 2 ve C 2’nin paralel bağlantısını göstermektedir . L 2’nin parazitik direncini temsil etmek için R 2 eklenmiştir .
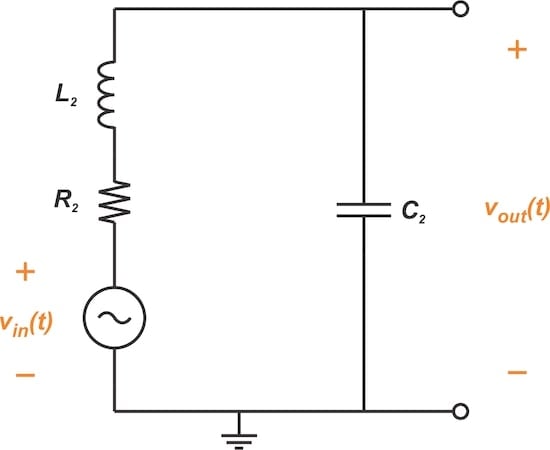
Şekil 3. Bir RLC devresinin örneği.
Bu tartışmanın amacı doğrultusunda aşağıdaki değerleri varsayalım:
L2 = 10 μH
R2 = 100 Ω
C2 = 25.33029 pF.
Bu, aşağıda hesaplandığı gibi 10 MHz’lik bir rezonans frekansıyla sonuçlanır:

Şimdi 10 MHz sinüzoidal bir giriş uygulayıp kapasitör üzerindeki voltajı çıkış olarak alıyoruz. Şekil 4, bir LTspice simülasyonunun sonucunu göstermektedir.
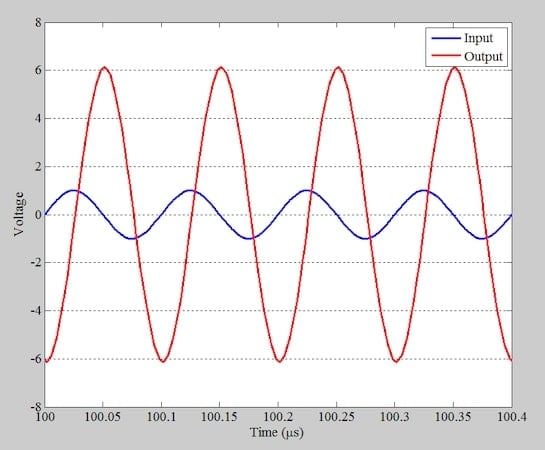
Şekil 4. 10 MHz sinyal için giriş voltajı (mavi) ve çıkış voltajı (kırmızı).
Giriş ve çıkış dalga formlarının zaman eksenindeki göreceli konumları, çıkışın girişle -90 derece faz farkı olduğunu açıkça göstermektedir. Bu, devrenin rezonans frekansında -90 derecelik bir faz kayması oluşturduğu anlamına gelir. Bunu matematiksel olarak doğrulayabiliriz, ancak bu makalede matematiksel kanıta girmeden perspektif kazanmak için simülasyon sonuçlarını kullanacağız.
Giriş frekansını 10,2 MHz’e çıkarırsak Şekil 5’teki dalga formlarını elde ederiz.
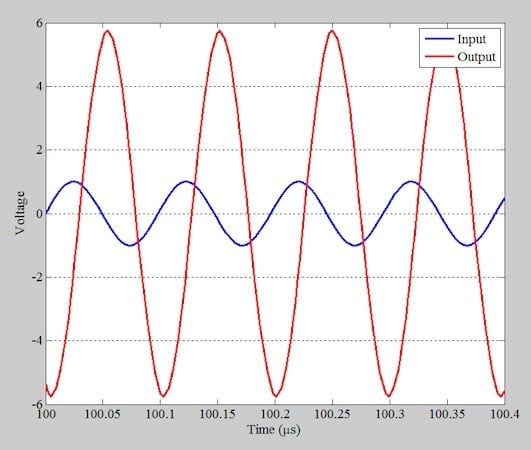
Şekil 5. 10,2 MHz sinyal için giriş voltajı (mavi) ve çıkış voltajı (kırmızı).
Rezonans frekansının üzerindeki frekanslar için, faz kaymasının mutlak değeri –90 dereceden büyüktür. Şekil 6, rezonans frekansının biraz altında olan 9,8 MHz’deki dalga formlarını göstermektedir.
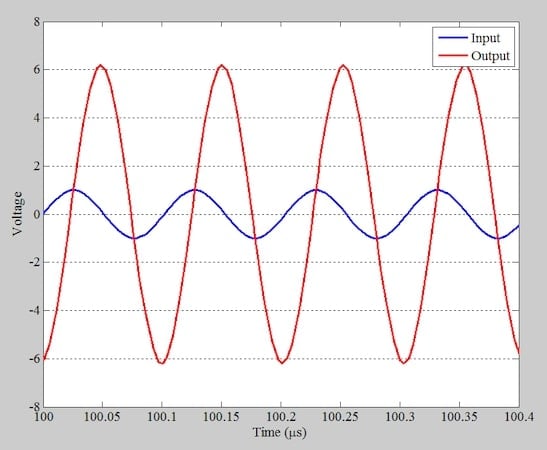
Şekil 6. 9,8 MHz sinyal için giriş voltajı (mavi) ve çıkış voltajı (kırmızı).
Rezonans frekansının altında, faz kaymasının mutlak değeri –90 dereceden küçüktür. Aynı sonuçlar, Şekil 7’de gösterilen AC analizi kullanılarak da elde edilebilir.
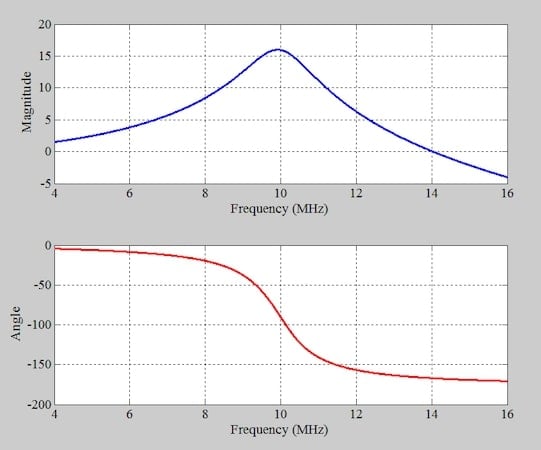
Şekil 7. RLC devresinin frekans tepkisi: büyüklük (üst) ve faz (alt).
Rezonans frekansı etrafındaki dar bir frekans bandında, büyüklük tepkisi neredeyse sabit kalırken, faz kayması frekansla yaklaşık olarak doğrusal olarak değişir. Bu frekansa duyarlı faz kayması, FM dalgalarını demodüle etmek için Foster-Seeley ayırıcısında kullanılır.
Çift Endüktörlerin Rolü
Şekil 8’de gösterildiği gibi, Foster-Seeley ayırıcısı, girişi seri RLC devresine uygulamak için bağlı indüktörler kullanır. Karşılıklı bağlı, çift ayarlı devre, yüksek birincil ve ikincil Q faktörlerine ve düşük karşılıklı endüktansa sahiptir.
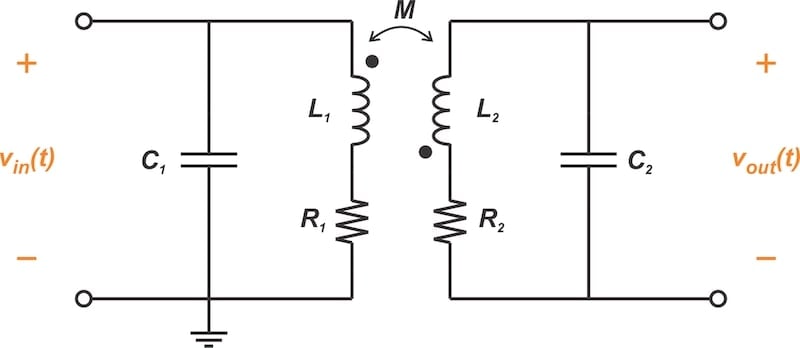
Şekil 8. Seeley-Foster ayırıcısında kullanılan bağlı indüktörler.
Devam etmeden önce, hem birincil hem de ikincil sargılarda kapasitörlerin kullanıldığını unutmayın. Bu, endüktörler arasındaki kuplajın birden az olduğunu gösterir. Eğer bir olsaydı, her iki tarafta tek bir kapasitör yeterli olurdu.
Basitleştirmek adına, L1’in seri direnci olan R1’in ihmal edilebilir olduğunu varsayıyoruz . Ayrıca, birincil devreye bağlanan empedansın , birincil öz empedansa göre önemsiz olduğunu varsayıyoruz. Sonuç olarak, birincil akım şu şekilde hesaplanabilir:

Birincil akım, sekonderde L2 ile seri bağlı bir gerilim kaynağıyla modellenebilen bir gerilim indükler ve bu da önceki bölümde incelediğimiz modele benzer bir sekonder devre modeli oluşturur. İndüklenen gerilim, iki indüktör arasındaki karşılıklı endüktansa ( M ) bağlıdır. Sargı yönlerinin negatif karşılıklı endüktans üretecek şekilde seçildiği varsayıldığında, indüklenen gerilim şu şekilde elde edilir:

Sekonderde görünen voltaj, V’ye göre zaten 180 derece faz farkı gösterir . Ayrıca , seri RLC devresinin rezonans frekansında -90 derecelik bir faz kayması ürettiğini biliyoruz. Rezonans frekansının üzerinde bu faz kayması daha negatif hale gelir. Rezonans frekansının altında ise faz kayması daha az negatif hale gelir.
Faz Kayması ve Frekans Arasındaki İlişkinin İncelenmesi
Devrenin genel faz kayması frekansa bağlı olarak nasıl değişir? Bunu üç olası duruma ayıralım: rezonans, rezonans altı ve rezonans üstü.
İlk olarak, rezonans durumunda, genel faz kayması, bağlı indüktörlerden 180 derece ve RLC devresinden -90 derecedir. Bu, 180 – 90 = 90 derecelik genel bir faz kaymasına yol açar.
Ardından, rezonans frekansının altında, RLC devresinin faz kaymasının –80 derece olduğunu varsayalım. Toplam faz kayması 180 – 80 = 100 derece olacaktır; bu da rezonans frekansının altındaki frekanslar için genel faz kaymasının 90 dereceden fazla olduğunu gösterir. –80 derece değerinin, devre davranışını belirlemeyi kolaylaştırmak için yalnızca bir örnek olduğunu unutmayın.
Rezonans frekansının üzerinde, RLC devresi için -100 derecelik faz kayması örneğini ele aldığımızda, 180 – 100 = 70 derecelik toplam faz kayması elde ederiz. Bu, rezonans frekansının üzerindeki frekanslar için toplam faz kaymasının 90 dereceden az olduğu anlamına gelir.
Bu sonuçları doğrulamak için Şekil 9’daki LTspice devresinde bir AC analizi gerçekleştireceğiz.
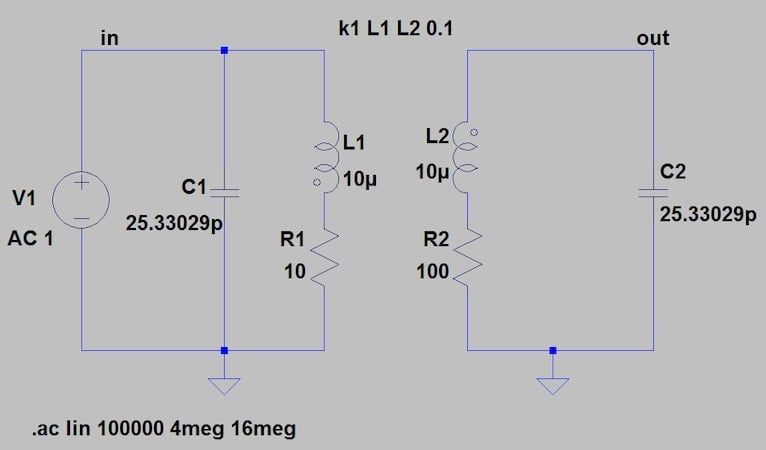
Şekil 9. Foster-Seeley ayırıcısının faz kaydırma ağını incelemek için LTspice şeması.
Yukarıdaki diyagramdaki K ifadesi , iki endüktör arasındaki kuplajı tanımlar. Daha önce belirtildiği gibi, Foster-Seeley ayırıcısındaki kuplaj 1’den küçüktür. Tutarlılık sağlamak için 0,1 gibi küçük bir değer seçtik. Şekil 10, AC analizinin sonuçlarını göstermektedir.
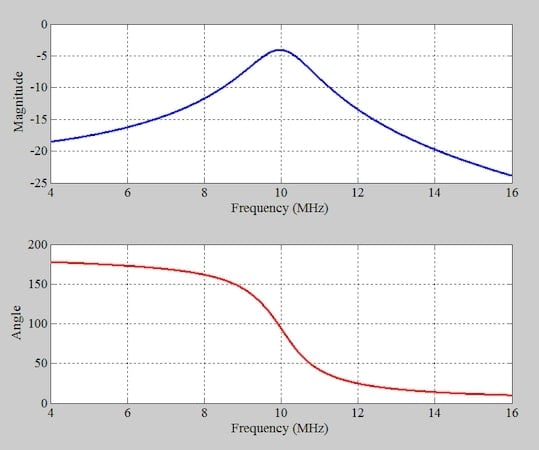
Şekil 10. Faz kaydırma ağının frekans tepkisi: büyüklük (üst) ve faz (alt).
Rezonans frekansında (10 MHz) faz kaymasının yaklaşık 90 derece, rezonans frekansının 90 dereceden fazla altında ve 90 dereceden az üstünde olduğunu görebiliyoruz.
Foster-Seeley Ayrımcısı
Artık temel bileşenlerini ele aldığımıza göre, Foster-Seeley ayırıcısını bir bütün olarak analiz etmeye hazırız. Kolaylık olması açısından, Şekil 11 şemayı yeniden sunmaktadır.

Cc ve C4 kondansatörleri RF’de kısa devre görevi görür. Bu nedenle giriş voltajı ( v in ) , RF bobini görevi görecek kadar büyük olacak şekilde seçilen L3 boyunca görünür.
İkincil sargı (L 2 ) iki bölüme ayrılmıştır. Yukarıdaki şekilde, A ve B düğümlerindeki gerilimler şu şekilde verilmiştir:
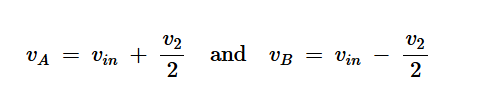
Burada v2 , L2 üzerindeki toplam voltajdır .
Önceki tartışmamızdan, v in ve v 2 arasındaki faz-frekans ilişkisini biliyoruz . Rezonans frekansında v 2 , v in’den 90 derece öndedir ve bu da Şekil 12’de gösterilen vektör diyagramını oluşturur.

ekil 12. Rezonanstaki gerilimlerin vektör gösterimi.
Diyot dedektörlerinin çıkışları ( v c ve v d ), v A ve v B’nin büyüklükleriyle orantılıdır . Genel çıkış ( v out ) şu şekilde verilir:
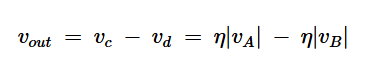
Burada η düzeltme verimliliğidir.
Rezonans durumunda, vA ve vB vektörlerinin eşit büyüklükte olması nedeniyle Denklem 5 sıfıra ulaşır . Rezonansın altında, sekonder uçlarındaki voltaj girişten 90 dereceden fazla öndedir ve bu da Şekil 13’teki vektör diyagramını oluşturur .

Şekil 13. Rezonansın altındaki gerilimlerin vektör gösterimi.
vA’nın büyüklüğü vB’ninkinden küçük olduğundan , Denklem 5 rezonansın altında negatif bir çıkış voltajı üretir.
Son olarak, giriş frekansı rezonans frekansının üzerinde olduğunda, sekonder uçlarındaki voltaj giriş voltajından 90 dereceden daha az öndedir. Bu, Şekil 14’teki vektör diyagramını oluşturur.

Şekil 14. Rezonansın üstündeki gerilimlerin vektör gösterimi.
Bu durumda vA’nın büyüklüğü vB’nin büyüklüğünden büyüktür , bu da rezonans frekansının üstünde çıkışta pozitif bir gerilimin ortaya çıktığı anlamına gelir.
Foster-Seeley Ayrımcısının Artıları ve Eksileri
Önceki makalede incelediğimiz dengeli eğim dedektörünün aksine, Foster-Seeley ayırıcısının her iki rezonans devresi de aynı frekansa ayarlıdır. Bu nedenle tasarımı daha kolaydır. Foster-Seeley ayırıcısı, frekans tepkisine daha az, oldukça doğrusal birincil-ikincil faz ilişkisine daha fazla dayandığı için üstün bir doğrusallık da sağlar.
Foster-Seeley ayırıcısının temel dezavantajı, girişte istenmeyen AM modülasyonuna karşı hassasiyetidir. Denklem 4 ve 5’e geri dönersek, giriş sinyalinin büyüklüğündeki değişikliklerin vA ve vB genlik değişimlerine yol açtığını görüyoruz. Bunlar da genel çıkışta genlik değişimlerine neden olur. Giriş sinyalindeki herhangi bir AM’nin demodüle edilmesini önlemek için, bu tür ayırıcılardan önce bir sınırlayıcı devre entegre edilmelidir.